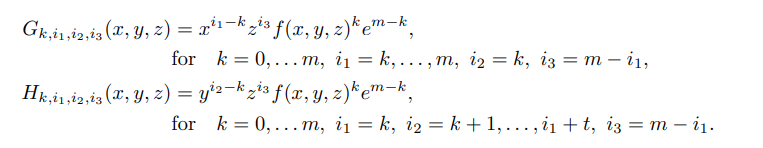杂题闲记-4

这次比赛有两道crypto，都是ECC相关的，第一道由于之前不了解Demytko体系，比赛期间并未找到paper，未能作出，赛后看了7feilee师傅发的paper才复现出来，第二题倒比较简单，分析出曲线的表达式然后发现在模N上是线性的即可解出。

Old Curse

这题使用的攻击方式是这篇paper里的攻击，本质就是对于e，N满足一个关系式和bound下的多元Copper Smith，多元Copper Smith的内容我之后专门单独写一篇，这里就不详述了，关系式和bound的定义如下

具体构造多项式的方法为（也是比较标准的xz-shift，yz-shift）：

规约完之后，取1，2，3行的多项式构成的理想，求Grobner Basis，再解方程即可求解，这里我还专门去学了一波Grobner Basis，然而事实上这题根本不需要，直接联立解这三个多项式即可得到解。

这样得到的解是\((p-s)*(q-r)\)，而通过ecm分解，可以得到其完整的素数分解，这样只需要遍历组合，即可得到\(p-s\)，然后再结合partial p的单元Copper Smith即可求解，需要注意的是，这题的数据卡的很死（看到7feilee师傅的epsilon是0.01，但我降到0.007才有解orz），small_roots需要调参的同时猜测下一个字母是什么。因为通过得到\(p-s\)，已经可以获知部分flag

b'Congratulations!Here is the flag:rwctf{tH3_CursE_h4S_bR0KEn_o1GIe\xb8\xc2T\xed\xd2}\xd1\xc9m\x8a\xdfE\xb0K[\x84\x93\xc9X9\xdb\x14p\x98\xce\x85=fD\x8e\x0c\xeb'

然后考虑olgie开头的字母，题给描述里有一个人名‘Olgierd’，故考虑下一个字母是r，于是猜测‘r’, ‘R’, ‘3’三种情况，逐个爆破即可通过partial p解出p，然后异或即得到flag，exp如下：

from Crypto_tools import *
from itertools import *


def matrix_overview(BB):
    for ii in range(BB.dimensions()[0]):
        a = ('%02d ' % ii)
        for jj in range(BB.dimensions()[1]):
            if BB[ii,jj] == 0:
                a += ' '
            else:
                a += 'X'
            if BB.dimensions()[0] < 60:
                a += ' '
        print(a)


def lattice_attack(pol, e, X, Y, Z, mm, tt):
    polys = []

    # G
    for kk in range(mm + 1):
        for i1 in range(kk, mm + 1):
            i3 = mm - i1
            poly = x ^ (i1 - kk) * z ^ i3 * pol ^ kk * e ^ (mm - kk)
            polys.append(poly)

    # H
    for kk in range(mm + 1):
        i1 = kk
        for i2 in range(kk + 1, i1 + tt + 1):
            i3 = mm - i1
            poly = y ^ (i2 - kk) * z ^ i3 * pol ^ kk * e ^ (mm - kk)
            polys.append(poly)

    polys.sort()
    monomials = []
    for poly in polys:
        monomials += poly.monomials()

    monomials = sorted(set(monomials))
    dims1 = len(polys)
    dims2 = len(monomials)
    M = matrix(QQ, dims1, dims2)

    for ii in range(dims1):
        for jj in range(dims2):
            if monomials[jj] in polys[ii].monomials():
                M[ii, jj] = polys[ii](x * X, y * Y, z * Z).monomial_coefficient(monomials[jj])

    matrix_overview(M)
    print('-' * 32)

    print('bound check:', abs(M.det()) < e ^ (dims1 * mm))
    print(int(M.det()).bit_length(), int(e ^ (dims1 * mm)).bit_length())

    BB = M.LLL()
    print('LLL done')
    print('-' * 32)
    matrix_overview(BB)
    print('-' * 32)
    H = [(i, 0) for i in range(dims1)]
    H = dict(H)
    for j in range(dims2):
        for i in range(dims1):
            H[i] += PR((monomials[j] * BB[i, j]) / monomials[j](X, Y, Z))

    H = list(H.values())
    PQ = PolynomialRing(ZZ, 'xq, yq, zq')
    for i in range(dims1):
        H[i] = PQ(H[i])

    xv, yv, zv = var("xq,yq,zq")
    print(solve([h_i(xv, yv, zv) for h_i in H[1:4]], xv, yv, zv))
    print('-' * 32)


N = 80330528881183983072964816732300543404856810562533626369319300810697262966387144944887576330528743612839739692299784591097332512948890518183519167192046959230085412831864255497489112175176914874596237618253755256608956517757030073479666104923402013469283716999320744856718736837534911809839541660207743594867
e = 78452652317506438607956636739779994986676384637399723342738736371812868831141251164966879331214017314432739387076791674001159059604426825547538902010774841189596518785149221523738464397224366361779781148300651051284198636694801404816891957209985325619623109930150535820404950711233032177848101830061155574970

PR = PolynomialRing(ZZ, 'x, y, z')
x, y, z = PR.gens()

alpha = 0.25
gamma = 0.15
delta = 0.15
beta = log2(e) / log2(N)

X = floor(4 * N ^ (beta + delta - 1))
Y = floor(3 * sqrt(2) * N ^ (0.5 + alpha))
Z = floor(N ^ gamma)

# Target polynomial
pol = x * y - N * x + z
mm = 3
tt = 1

lattice_attack(pol, e, X, Y, Z, mm, tt)

'''
[
[xq == r1, yq == r2, zq == -r1*r2 + 4298479533919222051278424008577823787364263332580438512213525069157290784423146604914451469507153913893839652272765256923591944212821123404914813182473920184304071161320177981959839398079746158378586359732136948418875022137978872858278664265291581144582621441419/3602343035298837553927542062227*r1],
[xq == 0, yq == r3, zq == 0],
[xq == r4, yq == (4298479533919222051278424008577823787364263332580438512213525069157290784423146604914451469507153913893839652272765256923591944212821123404914813182473920184304071161320177981959839398079746158378586359732136948418875022137978872858278664265291581144582621441419/3602343035298837553927542062227), zq == 0]
]
'''

y = 4298479533919222051278424008577823787364263332580438512213525069157290784423146604914451469507153913893839652272765256923591944212821123404914813182473920184304071161320177981959839398079746158378586359732136948418875022137978872858278664265291581144582621441419//3602343035298837553927542062227 + 1
x, z = var('x, z', domain=ZZ)

k1 = 3602343035298837553927542062227
k2 = 4298479533919222051278424008577823787364263332580438512213525069157290784423146604914451469507153913893839652272765256923591944212821123404914813182473920184304071161320177981959839398079746158378586359732136948418875022137978872858278664265291581144582621441419

res = solve([z * k1 == -k1*x*y + k2*x], x, z)
print(res)
print('-' * 32)

x = Integer(res[0].coefficients()[0][0])
z = Integer(res[1].coefficients()[0][0])

assert (x * y - N * x + z) % e == 0
u = (x * y - N * x + z) // e
v = x
w = -z

p_s_q_r = N - y
print('(p-s)(q-r) =', p_s_q_r)
print('-' * 32)

a = 3885193323999136856039629631403237736159969409639584250551518536355997978891524564035346751225719460630697433654700022473218421095180111760606245394708999
b = 944838399254930087523310357339939742097556483183482662977225295067404254966876247970295271959280809100126064366722912020666848894003017117276240476372364
E = EllipticCurve(Zmod(N), [a, b])
stone = E(5316297494616251967087180573684467112077977207314228196651011473838683480275875989908990738740861375687186766156200219641981169308660139151062711296717379891376294785675104640775506724244803337279235747630215478504380272738204733311972022712834357078381541224632797503360732934454187646031643331529389570159, 73177062713968648963738410812785853174528721431172461113561340178691492280271903912043554814810920745154304747328073913103230849027745226637330284520633847773874342467137552022725301429074046921710660867115557994943332628756632246059800601063580017261698262663178072317324978782579376388601713100806653808812)

d = inverse(e, p_s_q_r)
heart = d * stone

factors_list = [
    11,
    13,
    131,
    131,
    227,
    251,
    251,
    831396757,
    1108897087,
    2178767881,
    2253769513,
    2698180579,
    3504974177,
    3752390129,
    3787135097,
    4166580373,
    4192312919,
    505386797752007,
    15743834086867007131,
    14842292277078537617,
    15114820929537893567
 ]

base = 120659691081137900860528439558149439256036479214584879088476613192185895986414329679519081477454257879221194033908435726005914629
assert isPrime(base) == 1
assert base * prod(factors_list) == p_s_q_r
cipher = int(heart[0])

P.<x> = PolynomialRing(Zmod(N))
for num in tqdm(range(2, 12)):
    candidate = list(combinations(factors_list, num))
    for tmp_factors in candidate:
        tmp_pro = prod(tmp_factors) * base
        if 510 < int(tmp_pro).bit_length() < 513:
            for padding_bits in range(0, 264, 8):
                p_r = p_s_q_r//tmp_pro
                if b'rwctf' not in long_to_bytes(p_r ^^ (cipher>>padding_bits)):
                    continue
                else:
                    print('Found the p-r:', p_r)
                    print('-' * 32)
                    print('part flag:', long_to_bytes(p_r ^^ (cipher>>padding_bits)))
                    k = 512 - len('rwctf{tH3_CursE_h4S_bR0KEn_o1GIe') * 8

                    print('random padding bits:', k)
                    print('-' * 32)
                    for guess in tqdm([ord('R'), ord('r'), ord('3')]):
                        p_high = ((p_r >> k) << k) + ((guess ^^ 0xb8 ^^ 0x86)<<(k-8))
                        f = p_high + x
                        res = f.monic().small_roots(X=2 ^ (k-5), beta=0.45, epsilon=0.007)
                        if len(res) > 0:
                            print('found the result:', res)
                            p = p_high + int(res[0])
                            q = N // p
                            assert N == p * q
                            print(long_to_bytes((cipher >> padding_bits) ^^ p))
                            sys.exit()

最终跑个7，8min，得到flag

Homebrewed Curve

这里我是直接参考的Introduction to mathematical cryptography这本书里关于ECC的部分

结合标准ECC的公式推导证明，意识到\(\lambda\) 在点不同时表示的是两点间的斜率，相同时是该点切线的斜率，也即是曲线的导数，发现题给的公式里是\(2ax + b\)，故猜测曲线公式应为\(y = ax^2 + bx + c\)，同样使用原始ECC的证明方法，代入，即有\(\lambda X+v - (aX^2 + bX + c) = (X-x_3)(X-x_0)\)，其中\(x_0\)即为单位元点的x坐标，发现自洽，故确定了表达式。

又已知四个合法点，A，B，G，O，故做差求gcd即可得到P，得到P之后分析整个加法规则，可以发现\(x_3 = x_1 + x_2 - x_0\)，故\((kG)_x = k(G_x) - (k-1)x_0\)，即在模上满足线性关系，于是消去乘逆即可恢复，完整exp如下：

import random
import hashlib
from libnum import invmod
from Crypto.Cipher import AES
from Crypto.Util.number import *
from Crypto.Util.Padding import pad


class Curve:

    def __init__(self, **kwargs):
        self.__dict__.update(kwargs)

    def add(self, p1, p2):
        if p1 == self.zero:
            return p2

        if p2 == self.zero:
            return p1

        x1, y1 = p1
        x2, y2 = p2

        if x1 != x2:
            l = (y2 - y1) * invmod(x2 - x1, P)
        else:
            l = 2 * self.a * x1 + self.b

        x = ((l - self.b) * invmod(self.a, P) - self.zero[0]) % P
        y = ((x - self.zero[0]) * l + self.zero[1]) % P

        return (x, y)

    def mul(self, p1, n):
        if n == 0 or p1 == self.zero:
            return self.zero

        res = self.zero
        while n:
            if n & 1:
                res = self.add(res, p1)
            p1 = self.add(p1, p1)
            n >>= 1
        return res

    def gen_key(self):
        sk = random.randint(1, P)
        pk = self.mul(self.gen, sk)
        return sk, pk


a = 338105350242668308929697763396044301660
b = 70631159681042046635446173236982478064116538177970218795092411634131296885767
O = (
9754705134713370500425418962906364916694128219443986534870265438313712052553913556304578048773182865236181393234774811636563665254738358548547686098321918938336999994543320310489785839068889289585561389237322554300534800377365494547910434446171077511660646734142974631896227159038644834795595939445003783184271907835168083982210804135992472981458997056367475361358045062954295385753362817510369968941277639065938619221482008127361125972584968230982231483416783792258479416113581249377750311129019561848383083514672254514692875070293706012921153875918378772956871354902564753931679232128607231527456371560574893648150,
1568631189076775839914050721386821274436631828518639911590203429753674249963724465949098434816249858592209181914562366684848647341809527620103035336678319490054708958682690371323396425059326761139960520329829342510826324634871361342587962617109233961205192373716747727013613655062002124851676969800006190929713777159839273173689438005523473921392011053323705509027606365967531781465002057406686284573053674133382181877418753925610208463393821516137543581472014268533517599374830226690216017114664929426655189944119312800402788151756994817725042844409983509754618168400455155658767237036605650525875166823462486072842)

G = (
12532998589621080097666945122441206260965625062664570083674602252675892295679594034580389931735096079697125441246960301905307858329289188790029626634485829771734823159182904621402737540757430079518142479215838577833498703259391220160619426650385355407344355318793784733990238754982178179201863773450543367485332580658467529082154218982726945799974265641603861234501912638573835723384717842487988638277214429988591192513007462677389252245306874828268739787612245357189986581131725474432904172834643657027954405787429995826738074015516166702962206858859896933459093477305874443350335332968385035927605359630747331204285,
9677982578222119974363478748399786948047636069661692206522662047830643067492306311529114015320387572903840619331518584584400368845497864412752196098241604714699115186432809693851692194762433385961429711487895639093866274072187416400859677893102613898063134064507994013600600120524875666883108971040402000931357050726739367647257578379098507781478457700720118945453670136245178829199722575486626106268256525611370267664890630521019846806960099333376121482220389744953231843397729642415527736926160072478730239575933321480584291410141867063436921546657245313608614224909988684794138541856898030369431518091733072867437)

A = (
13487441097225225851381503721250882201348230291456769111220742564976603915541284733903445742010369949564133835184041848270925618065093927905336977954164490448790585095635629931682025014174873840946833423568776772534204109608898522472240761836716148677237778503440395160725865443571787537094238702604760374819569040510617361718394064021678094989416987996196517169045682067813960280671702291412278502544773112916378850480939772300572998243270196397238062178930871026435948325839912933370726600147757455774532767943291746849500590032985576917021393256167765909741347168603316800970606576192321995775188693736786445970160,
6017599616030668129613886703128129222334636061709939196813507723707943475088184604346025813500691639135280058944967720252980654491495661264318199620883475540203205404460632231139796107580037387665375828311005986158345466234113715267437612091657183380072338306002369357139146048822354864239891700619714889347124655297444781747932429314301652892318820172915980583258019186234125036141716353634569644160769758113796289362452914192384749373824618193948698071662955348463507865825856345882176096759589399552633775680285990970529819948425052395988810137569926613717988817522119415329098727602713461364878132364924903122354)
B = (
12325243140409509948390016947224835770037275709809199983863357504628092935405755615708471085146623088629930125222768275569249161772533262995997384602018963893791998430652960945216562316807507576074802113883850941124224565729858452198366295197883539144659809879585978117675682586217166877317417820588576087650344398633914868028869563804325425499084148917013752420468723286815504458371864930365680607878997170362726942929241087236675902387482097261010616327896296714705736419010609802542459944267215680522857179358080459237676786115966499799125501709118451402926712061906091422526053306629229053727883903005288795696508,
11505268856676087471457416848355426459576355205947042999067185842545620763588462278320812379117467263916383145249098261720386127003988544590766801168503624732272757534718035824926881081717465079216152838849559029603087971046414561166054241351336879142412362035493311540826692018441037485743070162688102587726966007813519178658355297714620527127226989353344537573502931404623687629851431286618067819135715913162892925109669537524861927815259765868576488623808219606831381696710149107337624587114848589866865509992514440834069577162069420625328534884840613305250527515798029474049312705531575693278171514006918716216130)

cipher = 0x1c002f8ecfa9177ffed879245681dbb606ed194f319c12a0a0940c7193e490095e9915d9ce9252f8377def6a92bcab6a
cipher = long_to_bytes(cipher)


# y = a*x^2 + b*x + c


def curve_f(point):
    x, y = point
    f = a * (x ** 2) + b * x - y
    return f


'''tmp1 = a * (A[0]**2 - B[0]**2) + b*(A[0]-B[0])
tmp2 = A[1] - B[1]
t1 = tmp1 - tmp2

tmp1 = a * (G[0]**2 - O[0]**2) + b*(G[0]-O[0])
tmp2 = G[1] - O[1]
t2 = tmp1 - tmp2
P = gcd(t1, t2)'''

P = 16964155551072495694293641975607630224727620299506094680698561697517114055981456463802735036670824528486635128253757386796419676408241481233714972382812783160754601985902695360703612064223677630625126592834772106201583720344150312382723959316671117708799304253580291408927697557459674805267132980104779404642276846095233729275890317878916892907703929715499923974553217760175425647369679697361138159243363407958468903965694813367459663590914481184614924748816307473556323329341018650081832249242635801731713869201574073433674020290004290751530577883843107369211669006291178070342858539229191025760918841972906522445981
assert isPrime(P)
c = 16964155551072495694293641975607630224727620299506094680698561697517114055981456463802735036670824528486635128253757386796419676408241481233714972382812783160754601985902695360703612064223677630625126592834772106201583720344150312382723959316671117708799304253580291408927697557459674805267132980104779404642230883341990354632152767094707323928211372322526675151193625579132448090680173107503198477462468656666566735425940700529384596061331818284884112463944986343599664280680261379848261768748456401895568843612967863345586540761447983568059191185623814855161140280703730793084066810882147924523685770382826268634431
assert (curve_f(A) - c) % P == 0

curve = Curve(
    a=338105350242668308929697763396044301660,
    b=70631159681042046635446173236982478064116538177970218795092411634131296885767,
    zero=(
        9754705134713370500425418962906364916694128219443986534870265438313712052553913556304578048773182865236181393234774811636563665254738358548547686098321918938336999994543320310489785839068889289585561389237322554300534800377365494547910434446171077511660646734142974631896227159038644834795595939445003783184271907835168083982210804135992472981458997056367475361358045062954295385753362817510369968941277639065938619221482008127361125972584968230982231483416783792258479416113581249377750311129019561848383083514672254514692875070293706012921153875918378772956871354902564753931679232128607231527456371560574893648150,
        1568631189076775839914050721386821274436631828518639911590203429753674249963724465949098434816249858592209181914562366684848647341809527620103035336678319490054708958682690371323396425059326761139960520329829342510826324634871361342587962617109233961205192373716747727013613655062002124851676969800006190929713777159839273173689438005523473921392011053323705509027606365967531781465002057406686284573053674133382181877418753925610208463393821516137543581472014268533517599374830226690216017114664929426655189944119312800402788151756994817725042844409983509754618168400455155658767237036605650525875166823462486072842),
    gen=(
        12532998589621080097666945122441206260965625062664570083674602252675892295679594034580389931735096079697125441246960301905307858329289188790029626634485829771734823159182904621402737540757430079518142479215838577833498703259391220160619426650385355407344355318793784733990238754982178179201863773450543367485332580658467529082154218982726945799974265641603861234501912638573835723384717842487988638277214429988591192513007462677389252245306874828268739787612245357189986581131725474432904172834643657027954405787429995826738074015516166702962206858859896933459093477305874443350335332968385035927605359630747331204285,
        9677982578222119974363478748399786948047636069661692206522662047830643067492306311529114015320387572903840619331518584584400368845497864412752196098241604714699115186432809693851692194762433385961429711487895639093866274072187416400859677893102613898063134064507994013600600120524875666883108971040402000931357050726739367647257578379098507781478457700720118945453670136245178829199722575486626106268256525611370267664890630521019846806960099333376121482220389744953231843397729642415527736926160072478730239575933321480584291410141867063436921546657245313608614224909988684794138541856898030369431518091733072867437),
)

assert curve.mul(curve.gen, P) == curve.zero

# kGx - (k-1)*Ox
ck, C = curve.gen_key()
assert (ck * G[0] - (ck - 1) * (O[0])) % P == C[0]

bk = ((B[0] - O[0]) * inverse(G[0] - O[0], P)) % P
shared = curve.mul(A, bk)[0]
key = hashlib.sha256(long_to_bytes(shared)).digest()
aes = AES.new(key, AES.MODE_ECB)
print(aes.decrypt(cipher))