整体思路
利用构造多项式技巧,构造出多项式,形成一个格,然后进行规约,得到较小范数的多项式,然后通过结式求解(有时也有其他办方,比如直接系数gcd,多项式gcd或是Gröbner basis等,May’s origin attack on CRT-RSA就出现了好几种方法)小范数多项式,即可得到原多项式在一定范围下的所有根。本质思想其实就是把有限域上的方程转化到整数域,而转化的界限就是由柯西-施瓦茨不等式给出的。
理论基础
Howgrave-Graham’s Lemma

此定理的意义在于,如果找到了符合约束的多项式\(h\),则\(h\)在模\(N\)上的所有小根也即是\(h\)在整数域上的所有小根,也就是说,我们可以将有限域上的多项式转化为整数域上的多项式。
LLL
即是格基约化,这里的作用即是通过对构造出的特定的格的约化而产生符合约束的多项式\(h\),然后通过结式将多元方程转化成一元方程式,之后解整数域上的一元方程即可。
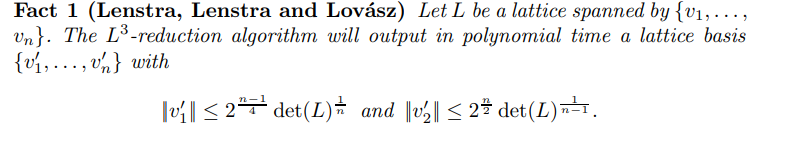
通过以上事实,可以看到LLL至少可以找到两组满足约束的向量,也就保证了在规定条件下结式有解的可能性。
构造多项式
Jochemsz-May Strategy
Modular
Basic Strategy
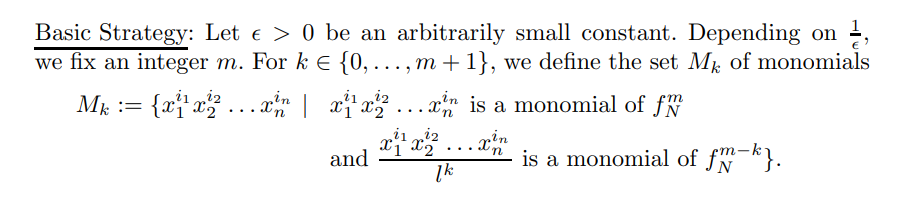
先算出m及\(f_N^m\),然后使\(k\)遍历\([0, m]\),计算\(M_k\),指定\(l\) 并根据以下公式,计算多个多项式,构成格基。
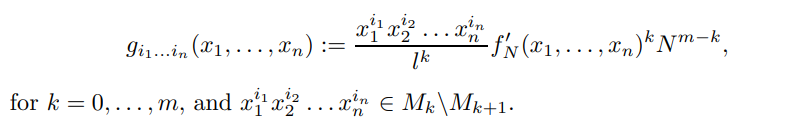
例子如下
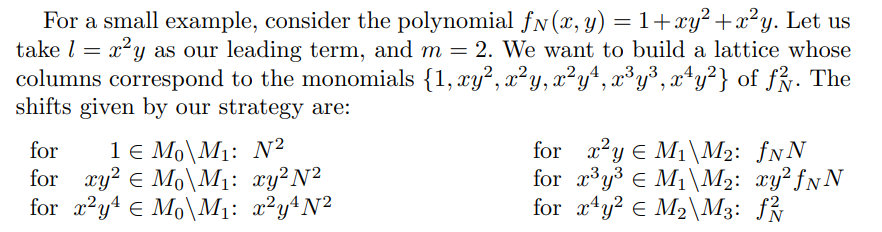
这样的构造是为了保证,最终构造的多项式里的每个单项式都是\(f_N^m\)中的单项式。
要注意的是,并不是说构造出来的多项式需要严格是以上形式,这只是提供了一种总体构造思想。
Extended Strategy
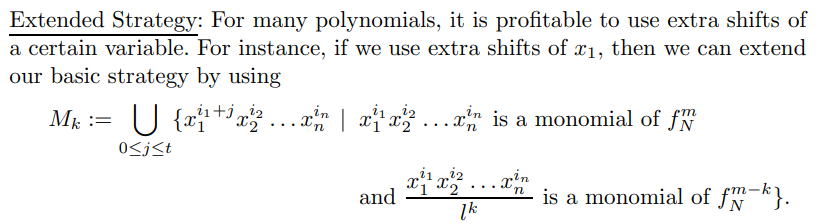
针对某个变量的extended strategy,是为了得到更好的界,有时也可以通过一些关式构造出新的变量用来shift。
相关知识学习
Gröbner basis
仿射簇与理想

可以看到仿射簇是一组多项式公共根的集合。
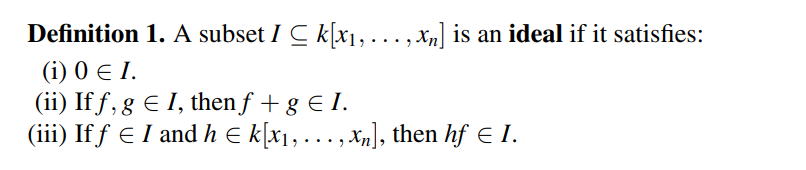
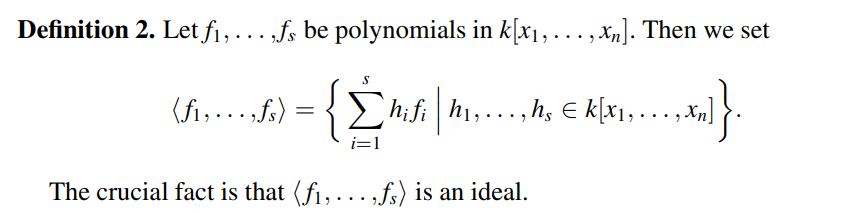
理想与子空间类似,不同的是子空间我们使用标量相乘的线性组合,而理想使用多项式相乘的线性组合。
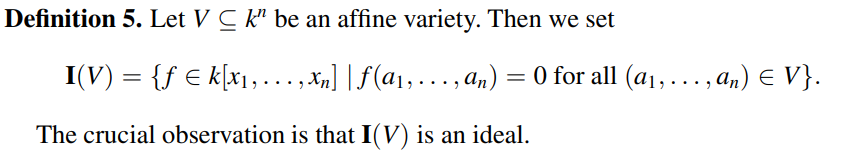
可以根据一个仿射簇的所有根来定义理想,其内所有多项式的根均包含仿射簇中所有根。
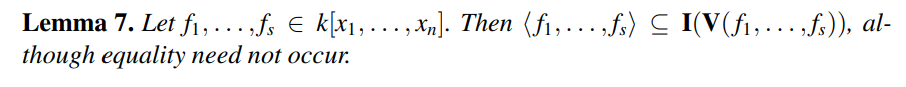
可以根据仿射簇定义理想,同样可以根据理想定义仿射簇,但通过这样的嵌套的结果不一定总是相等。
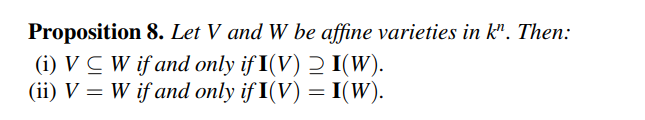

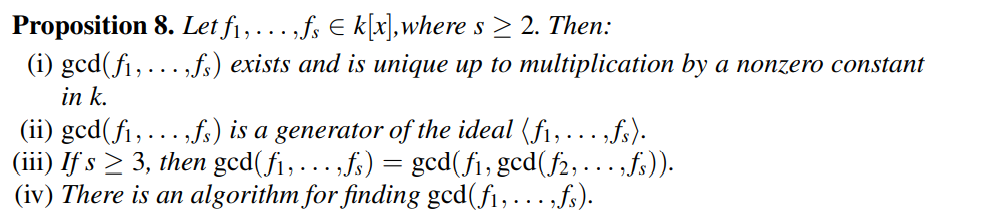
多项式间gcd性质与整数基本一致

序与单项式理想
由于通过总结多项式除法和高斯消元法,意识到‘序’的意义,故这里定义多元单项式的一种比较的序。
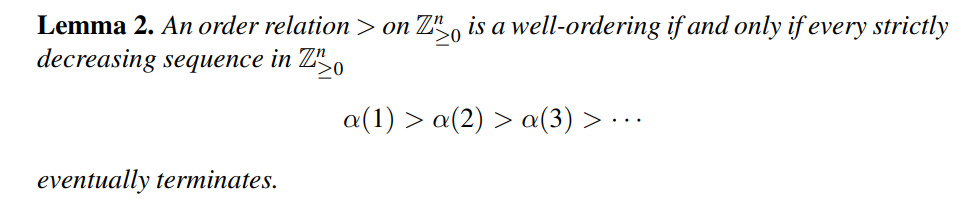
同时我们知道定义一个序是好的,当且仅当它不存在无穷递减序列。

这里通过比较向量差的首个非零向量来作为一个序(此即lex order,类似于字符串的字典序比较法)
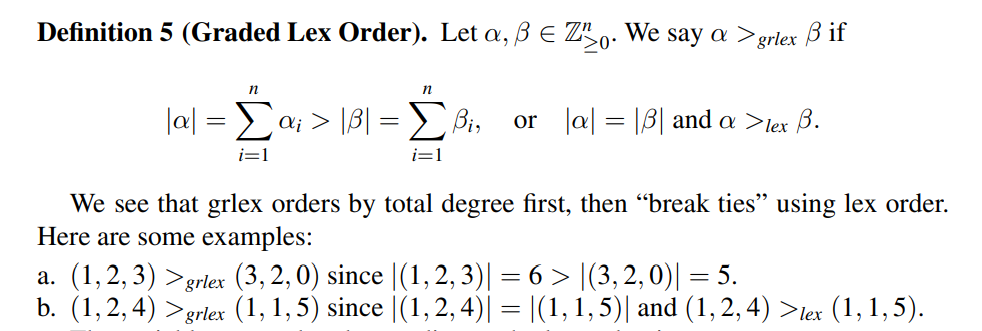
考虑到纯字典序有不妥,这里将向量的范数也引入,优先以范数比较,再其次以字典序比较
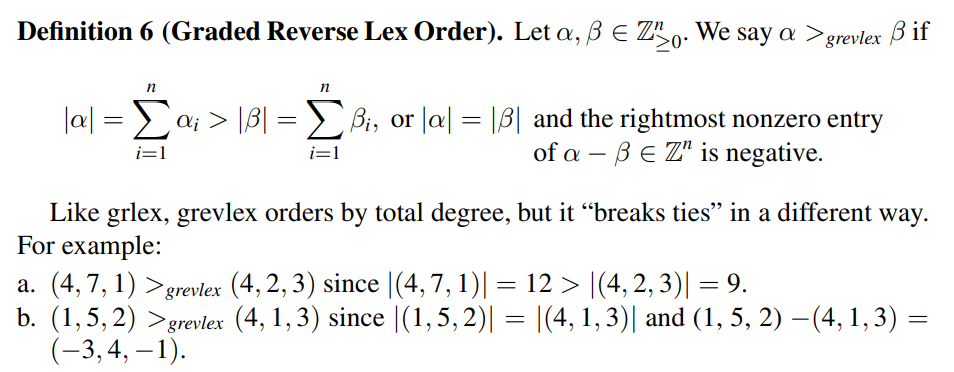
也可以定义反向字典序(即从最右边变量开始比较,且最右边小的在前面)

对于一个多项式,定义诸多概念如上
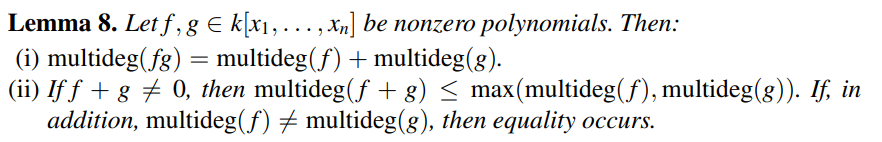
于是有朴素的定理如上。

这里定义了多元变量的多项式除法,主要点在于除的对象是一组多项式,具体操作与单元多项式除法类似,通过leading term判断是否结束除法,依次除各个多项式即可。若\(f\) 对于\(f_1, f_2, \dots,f_s\)做除法余数为0,则\(f \in <f_1,\dots,f_s>\),即\(f\)属于由这组多项式生成的理想。于是考虑想找一种好的basis,使得任意多项式除此basis的余数唯一确定。

定义无系数的“单项式理想”,这里建议结合wiki看着理解,单纯概念感觉这里介绍的有点不是很清晰,定义单项式理想的目的是方便刻画Grobner Basis。一个多项式属于一个单项式理想当且仅当它的每个项都可以被此理想的基中的一个项整除。
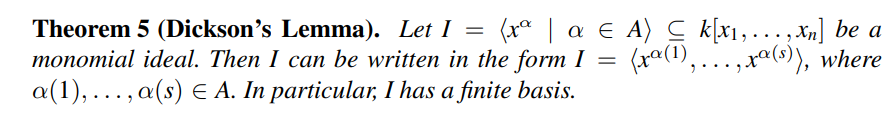
单项式理想可以有限生成
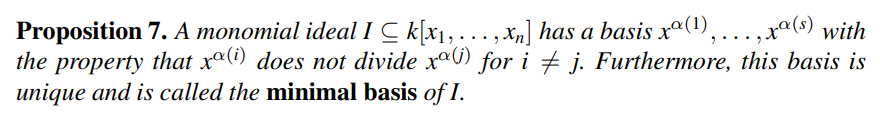
定义了单项式理想上的最小基
Grobner Basis

定义了由首项生成的理想,需要注意的是\(<LT(f_1), \dots,LT(f_s)>\)和\(<LT(I)>\)
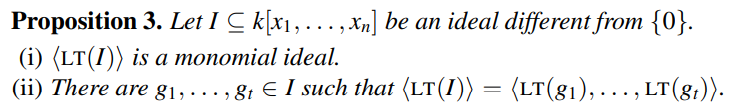
关于Grobner Basis存在性的定理

给出了Grobner Basis的定义

此即是由Hilbert定理得出的,任意多项式环可以有限生成。

这里表面了在Grobner Basis下余多项式的唯一性,证明仍是标准的反证结合定义即可,这也顺其自然的推出了一个多项式的余多项式为0和其属于理想的等价性。

定义一个表示对于basis余多项式的表示方法。
Grobner Basis之所以可以用于解多元方程,在于其会将多元分离,即只要方程数量保证,产生的基中变量是依次递增,即从1到n,由此可以依次求解各个方程,得到各个变量,类似于对多项式构成的矩阵做了一个上三角化。
推荐阅读论文
- A Strategy for Finding Roots of Multivariate Polynomials with New Applications in Attacking RSA Variants
- New attacks on RSA with small secret CRT-exponents
- Approximate Integer Common Divisors
这些论文里出现的参考文献都可以跟进阅读,加深理解。
相关论文勘误
Cryptanalysis of Unbalanced RSA with Small CRT-Exponent | Alexander May
在module e的attack中最后的例子矩阵中
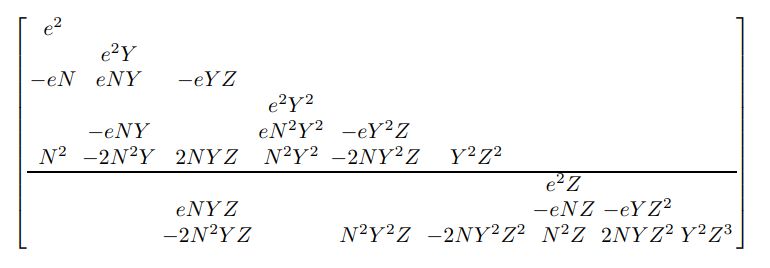
矩阵第五行,第四列元素错误,应为\(eNY^2\),而非\(eN^2Y^2\),我一开始写代码没套多项式生成,直接搬的矩阵,导致bound严重不符合,最后发现这里多了个N。