Way to Crypto

Pre Algorithm

link1

link2

tips1:注意BSGS算法的局限性，即\(gcd(a,p) = 1\) ，条件不成立时，需使用扩展BSGS或其他算法。

tips2:Linux下分解工具 primefac

tips3:推荐使用工具sage，需在linux下配置，其包含了很多库和函数，如cypari2等，sage官方文档，cypari2官方文档

RSA

淘宝师傅博客，总结的很好，可以当作索引来学习。

虽然说是RSA，但其实涵盖了有限域上的离散对数密码体系和大整数分解密码体系的知识，只是这些知识可以较好的通过RSA这个模板呈现出来。

Given(e,d,n)

tips：博客内给出的NCTF2019 babyRSA其实并不是这种情况，而是利用p，q接近，开根phi求解的。

Given (p, q, dp, dq)

tips:博客给出的证明其实就是CRT的证明

Wiener Attack

tips1：博客中给的证明开始的一步有问题，可以结合此篇文章一起看，本质上其实就是利用了连分数的最佳逼近性质和的d较小的漏洞。

tips2：题中的rational_to_quotients函数即是计算连分数中的数列，原理比较简单，自行推导即可。convergents_from_quotients函数是用来计算每一级连分数的，即最佳逼近。

Coppersmith 常见相关攻击

tips1：此部分推荐先把wiki部分内容看过一遍再做扩展，可以配合github上的这个项目理解，此处方法不理解的地方，建议多打打草稿，画一画就懂了，每种情况都可以切实code一下，至于根本原理，个人觉得不一定非要十分清楚，会意即可，感兴趣的可以参见此篇文章。

一定要搞清楚small_roots函数（sage的small_root传参X不能过大，如果X过大，即使存在X内的解，也无法求出）：

下面贴出测试代码：

from Crypto.Util.number import *

base = 512
p = random_prime(2^base, 2^(base-1))
q = random_prime(2^base, 2^(base-1))

e = random_prime(2^6, 2^4)				# for test partial d
# e = random_prime(2^25, 2^23)  			# for test partial p 
# e = 7							# for test partial m 

assert(gcd(e, p-1) ==1 and gcd(e, q-1) == 1)

n = p * q
m = bytes_to_long(b'flag{Test_flag_for_LordRiot}')

c = pow(m, e, n)

print('p = ' + str(p))
print('q = ' + str(q))
print('n = ' + str(n))
print('e = ' + str(e))
print('c = ' + str(c))

R.<x> = PolynomialRing(Zmod(n))


# this situation should use with a small e
def partial_m(k1, k2):
	m_high = (m >> (k1+k2)) << (k1+k2)
	m_low = m & (2 ^ (k2+1) - 1)

	wait = (m - m_high - m_low) >> k1
	assert(m_high + wait  * 2 ^ k1 + m_low == m)

	assert(wait < n ^ (1/e))

	f = (m_high + m_low + x * 2 ^ k1) ^ e - c
	solve = f.monic().small_roots(X=2^k1, beta=1)
	x0 = solve[0]

	print(long_to_bytes(m_high + x0 * 2 ^ k1 + m_low))
	


def partial_p(low_bit, leak_bits, phar=0, _beta=0.4, test=False):

	if low_bit:		
		if test:
			phar = p & (2 ^ (leak_bits+1) - 1)	
		assert((p - phar) >> leak_bits <= 2 * n ^(1/4))					
		f = x * 2 ^ leak_bits + phar		
		solve = f.monic().small_roots(X=2^(base - leak_bits), beta=_beta)
	else:	
		if test:					
			phar = (p << leak_bits) >> leak_bits						
		assert(p - phar <= 2 * n ^(1/4))
		f = x + phar
		solve = f.monic().small_roots(X=2^leak_bits, beta=_beta)


	x0 = solve[0]
	p_solve = int(x0 * 2 ^ leak_bits + phar)
	q_solve = n//p_solve
	print(p_solve * q_solve == n)

	d = inverse(e, (p_solve-1) * (q_solve-1))
	print(long_to_bytes(pow(c, d, n)))
	return p_solve


# cause the partial_p function need little k, so we may need to reduce the p0
def partial_d(k, second_bits = (base * 2) // 6 ):
	assert(k>0)
	kbits = k + int(n).bit_length()//4
	d = inverse(e, (p-1) * (q-1))
	dhar = d & (2 ^ (kbits + 1) - 1)
	solved = False

	X = var('X')
	for k in range(1, e+1):
		results = solve_mod([e*dhar*X - k*X*(n-X+1) + k*n == X], 2^kbits)
		for x in results:
			p0 = int(x[0])
			leak_bits = p0.bit_length()
			if p0 == p & (2 ^ (leak_bits+1) - 1):
				print("leak p bits: " + str(p0.bit_length()))

				try:		
					p_solve = partial_p(true, p0.bit_length(), phar = p0)
					if p == p_solve:
						print('Got the solution!')
						solved = True
						break
				except:
					continue
		if solved:
			break
	if not solved:
		print("No solution found")


# partial_p(true, 300, test=True)
# partial_m(50, 50)
# partial_d(50)

tips2：使用的sage脚本中的small_roots其实即是集成了LLL算法的函数。

e与phi不互素

NCTF 2019 easy-RSA，writeup

涉及有限域开高次根问题，值得细看。

（其实RSA算法即可以看作是在求\(GF(n)\)下的\(e \ th\) root，但\(gcd(e, phi) = 1\)。）

这篇文章讲的挺好，算是汉化并解释了一波论文

AMM（Adleman-Manders-Miller）算法： （论文中关于推导方面有将q写为p的笔误，需注意）

$for  s * r^t = q-1,  $ 为\(\delta \mod q\) 的一个\(r\)次非剩余，则有

​ \(\delta^\alpha (\rho^s)^{\sum_{i=1}^{t-1}j_i*r^{t-1-i}}\)

为\(\delta\)的r次剩余。

算法流程：

至于如何生成所有的r次剩余（即r个r次剩余），则可以通过以下公式：

​ \((x^{\frac{q-1}{r}}) ^ r \equiv 1 \pmod q\)

在q的剩余系内，取r个不相同的x，则得到r个r次剩余，即全部解：\(m_0 * x_i^{\frac{q-1}{r}}, \ i \in (1, 2, \dots, r)\)

gcd(p-1, q-1)过大

此处关于\(x^{N-1} \pmod p\) 最多有a个值，可以从ord考虑将\(x^b\)看成一个整体，考虑其阶数为\(ord//g\)，可知为原根时，可取到a，非原根时小于a。（本质是判断r次剩余的解有\(gcd(n, \phi(n))\)个）

RSA-CRT体系攻击

RSA-CRT介绍

使用的LLL掌握矩阵构造即可，具体可以看这篇paper

Copper Smith原理

soreatu师傅总结了一篇Copper Smith的编年的paper索引， 可以当作paper目录使用

Copper Smith 根本思想：

构造某个多项式商环（需要将\(GF(n)\)上的多项式转换到\(Z\) （实际上可能先是\(n^m\)上）上），取其上所有的多项式的系数构造Lattice，之后进行某种初等变换，之后通过对其中某个block matrix（也可能是整体）的规约，得到一组性质好的等价的多项式的系数，从而求解。

推荐看这篇survey，对一些概念讲的比较详细，相对于Copper Smith最初的论文更容易理解。

Copper Smith基础

理论基础：

此即Howgrave-Graham定理，证明了构造符合规则的多项式\(g(x X)\)后，最终欲求的性质较好的解向量可以通过格基约化找到。

在利用单元变量构造Lattice时，构造规则为：

对于\(x^i*p(x)^j\)中的\(i, j\)，使用 $(i, j) = hk + i + (j-1) k \(， 来计算对应的列坐标，即对于\)p(x), i = 0, j = 1\(，此多项式各个参数即在矩阵的第\)(i, j) = h*k$ 列作为矩阵元素，具体的行坐标即为多项式内\(x\) 不同指数相对应。

以原论文中第6列为例：

\(p(x) = x^2 + ax + b\) 对应\(h*k = 6\)，观察可发现第六列的元素即为\(b, a, 1, 0, 0, 0, 0\)， 即对应\(x^0, x^1, x^2, x^3, x^4, x^5\) 的系数。

之后构造向量r，使得\(s = r M\)，向量s的右部分全为0。

注意此后的矩阵\(\widetilde M\) 为对M矩阵进行初等变换后的矩阵，而矩阵\(\hat M\) 为矩阵\(\widetilde M\) 左上角\(h k \times h k\)的分块矩阵，而由于构造，故有\(det(\hat M) = det(\widetilde M) = det(M)\)， 而格基约化的对象为矩阵$det(M) $。

论文的以下部分是在论证欲求的解向量在\(\hat M\) 所形成的Lattice上

以下部分说明了必然存在一个线性组合\(f_g\)，使得\(\sum_g f_g d_g = 0\)，也就产生了一个格上的short vector，而最终通过LLL约简出的short vector即是\(f_g\)， 之后正常解方程即可

需要注意的是对于不同的多项式，构造矩阵时存在着不同形式的优化，例如sage中集成的small_roots构造的单变量矩阵便与Copper Smith最初论文中的矩阵有所不同。

github的这个项目，便使用的是如下构造方法：

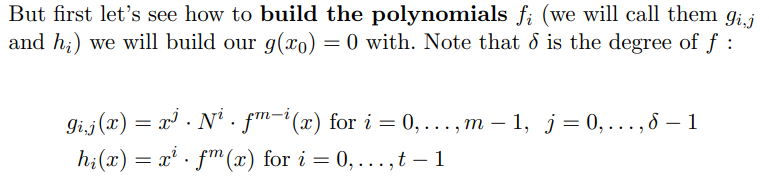
Copper Smith延申

1. 模N未知：

   ​ 其实最早学习Copper Smith的时候，对于partial_p和partial_d的情况我就很疑惑，不像partial_m，这两种情况似乎并没有给出一个模N上的等式，而事实上，Copper Smith确实是可以作用于不确定的有限域上的。

   以partial p情况为例：

\[ |\hat p - p| < N^{\frac{1}{4}} \\ \Rightarrow \hat p \equiv x_0 \mod p \\ \Rightarrow f(x) = \hat p + x \equiv 0 \mod p\\ known:\hat p, \quad p > N^\beta , \ \beta \in (0, 1] \quad x < X\\ \]

我们仍然按照之前的形式构造多项式：

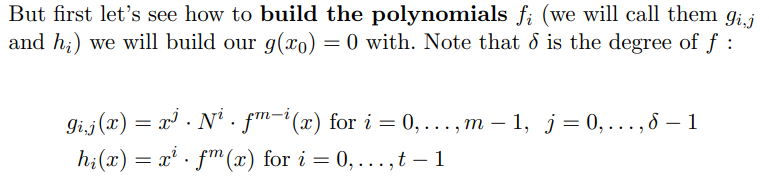
那么第一种多项式在模\(p^{m-i} N^i = p^m * q^i\) 上为0，将\(q^i\)看作常数，即为在\(p^m\)上为0，第二种多项式亦为在模\(p^m\) 上位0，符合Howgrave-Graham定理的条件，即可约简出一组较好的基。

而不同之处在于对根范围的计算，需要将\(p\) 替换为\(N^\beta\)，剩余步骤与已知N情况相同，最终得到约束：

2. 多变量情况

   先从二元谈起，可以看这篇paper

   ​ 讲的很详细，虽然略去了不少证明，但是可以比较直观的认识到多元Copper Smith的本质也是先shift多项式的阶，再使用格基约化将模方程降维，从而更容易的求解，与单变量并没有本质的区别。

   ​ 多元的构造方法，可以参见这个多元Copper Smith的脚本，原blog是韩文写的，看着很难受，这里大致阐述一下构造方法，以2变量为例：

   solve函数中的参数m代表shift的阶数，t代表初始多项式的阶数，这里使用

   \(p_1 * 2^{k_1} + p_2 *2^{k_2} + p_3*2^{k_3} = p\)

   ​ 已知\(p_2, p | N, N\)，求p1，p3，可以看到多项式阶数为1，shift一般可选用变量数乘2，此处为4

   ​ 最终构造\(T\) 个多项式，\(T\) 为n个元素，和小于等于m的全排列数量（这点其实可以从n维空间去考虑，即在n维空间构造一个半径为m的球，取其中所有整数点，即返回了T个n维向量，每个向量即为\((e_1, e_2, \dots, e_n)\)，其中\(e_i\) 即为下式中\(e_i\)）

   构造n个多项式如下：

   \(g(x) = f(x)^k * \prod_{i = 1}^{n} x_i^{e_i} * N^{max(t-k, 0)}\)

   以每个多项式中各个变量的系数为矩阵元素，可以看到构造的多项式是在\(GF(N^{max(k, t)})\) 上的。

   这里为了加深理解，推荐看看这篇论文，即是Boneh and Durfee attack

   关于多元Copper的整体结构之后会单独写一篇文章来说。

Lattice

2012 Biu Crypto Lattice

b站有中英翻译视频，直接搜索即可

纠正：

1. Introduction，49：00，所乘幺模矩阵除对角线外应为0，而非1

Introduction to Lattice

1. 格基等价条件：

   1. 换序：\(V_i \leftrightarrow V_j\)
   2. 相反：\(-V_i \leftarrow V_i\)
   3. 齐次：\(V_i \leftarrow V_i + kV_j\)

   证明简单，此处略，此三种映射均可使用幺模矩阵（幺模矩阵对乘法和求逆封闭）描述。

2. 空间映射到格基：

   通过规定基础平行多面体：\(P(B) = \{a_1x_1,a_2x_2,\dots, a_nx_n | a_i\in[0,1) \}\)，将空间任意点均可映射到此结构中.

3. 格的行列式定义：

   \(for\ L(B),\ det(L) = det(B) = S_B\)

   B即为格的一组基，\(S_B\)为基础平行多面体的面积，基础平行多面体中有且仅有一个格点，故可用来描述格的密度。

4. 最短向量\(\lambda_1(L)\) （这个定理非常重要，很多时候需要通过其算bound）:

   利用正交化求出其下界\(min\{\hat{v_i}\}\)，根据Minkowski's Theorem的推论得到上界\(n^{\frac{1}{2}} det(L)^{\frac{1}{n}}\)

Reduction for SIS

1. SIS问题：

   $for  vectors:  a_1, , a_n, find  z_1, , z_n $

   \(meet: z_1*a_1 + \dots + z_n*a_n = 0 \ | \ z_i \ in\ \{-1, 0, 1\} \ \ \ a_i, z_i \ in\ Z_q^n\)

   \(z_i\)的范围越小，越难解出，简单考虑可知整数解集对加法有封闭性，故而构成一个格

   （容易想到利用LLL解决背包问题的情况）

2. 格上的高斯分布：

   1. 对于区域A，若其选点上均匀分布，其Gram-Schmidit正交的基也均匀分布。

   2. 若一个基础平行多面体上均匀分布，则每个格基构成的基础平行多面体选点均均匀分布。 这里的含义是，对于整个\(R^n\)空间上的某个高斯分布的点集，在每个满足以上条件之一的区域内均为均匀分布，即选到任何一个点的概率相同。可以结合以下MATLAB代码理解正态分布在一个方差上界下的光滑性：

   for ceita = 1.25:0.005:1.3
       x=0.00:0.01:1.00;
       y = normpdf(x-100,0,ceita)
       for n = -100:1:100
           y = y + normpdf(x+n,0,ceita);
       end
       figure
       plot(x,y);
   end

3. 基于高斯分布的规约算法：

   ​ 本质即是对于随机的一个格点，以其为高斯分布的原点（即期望），根据设定好的高斯分布在其附近取一点（此处由于格点是离散的，所以存在一个取整处理）。由于基于高斯分布，故所选向量距离原点的距离期望会较小，从而找到一个较小的向量。高斯分布的方差会在限定范围（即上面所提约束条件）内移动，直至找到一个足够短的向量为止，为了找到短的向量，同时满足点的随机性，方差应该较小，但又不能低于某个限度。

   ​ 讲座中其实已经足够直观了：

   

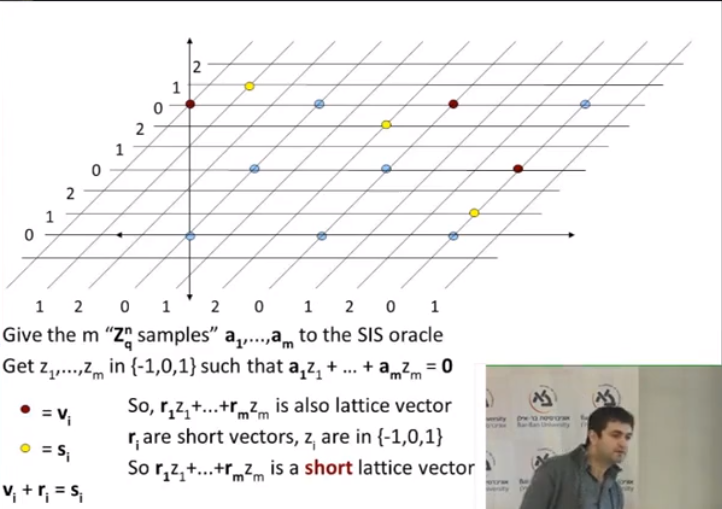
Introduction-to-Mathematical Chapter 6

如果BIU冬令营都听懂了，其实中间（指6.3-6.5）关于格的介绍部分就可以都不看了，直接跳到6.6就行，也可也结合6.5具象化的理解基于高斯分布的规约算法。

Babai's CVP solve algorithm

基于正交基的解决CVP算法，只有基底正交性足够好时，才可以解决CVP问题。

算法过程即是将目标向量表示成正交性好的基底的组合，对系数求最接近取整，得到的向量即为一个与目标向量非常接近的格上向量。

Hadamard's ratio：描述基底正交性的量，越接近于1，正交性越好。

GGH

GGH基于了CVP问题，利用Babai's Algorithm来实现，需要在较高维度实现，否则可以使用规约算法（如LLL）找出一组正交性很好的基底。

卷积多项式环

多项式环上的乘积运算，其实可看成级数乘法（梦回史济怀）：

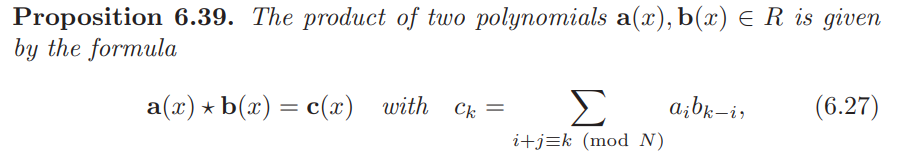
N控制指数的域，q控制系数的域。

将\(R_q\)上环lift到\(R\)上环，常采用的方法：将\(0, 1, \dots, q-1\)映射到\(\lceil-\frac{q}{2}\rceil, \dots, \lceil\frac{q}{2}\rceil\)上。

NTRU

NTRU系统本身其实代表着一个较为泛的理念，实现较为简单，且其可以在多个层面实现，多项式/整数等等，可以参见书中描述或此篇博文，即可以基于多项式，也可也基于整数。

NTRU的q估值问题（根本原因是因为先后所处有限域为p，q，不相同，故而a(x)需要小于q，否则会被截断），由于往往很难达到最大情况，所以其实一般取一个较小q以提高效率，并保证错误率较低即可。

NTRU系统的破解可以从自构造私钥入手，通过推导不难发现，如果找到一组\(f(x), g(x)\)，满足\(f(x)*h(x) \equiv g(x) \pmod q\)，并且\(f(x), g(x)\)的系数较小（为了使\(f(x)*m(x) + p * g(x)*r(x)\)较小，不被截断），且在\(Z_p\)下可逆，则可以解密，但需要注意的是，碰撞的概率非常小，且得到不是原有私钥簇内元素（即通过乘\(x^k, k=1,2,\dots,q-1\)生成的簇）的概率更加小。

NTRU系统的安全重点在于前后不同有限域（\(G_p, G_q\)），故而需要考虑截断问题

格基约化

1. 二维上的高斯约化：

   

   这样可以求得一组最小且正交性好的基，不过仅适用于二维情况。极小性由\(v_1,v_2\)之间大小及系数m保证，正交性由每次的系数m保证，具体证明看书上的即可，写的很详细。

2. LLL算法：

   通过施密特正交化和condition判断，得到一组正交性好的基，同时其中的最短向量为格上的较短向量，可以解决近似SVP和近似CVP。

   

   扩展LLL：BKZ-LLL，sage中也有集成:

   # 调用格式如下，L为格矩阵，通常取格维度的1/10左右作为block大小即可
   L.BKZ(block_size)

密码分析中的格基约化

包括NTRU、背包、GGH等问题的格基约化破解，书上例子较为详细，结合习题理解即可。

CTF中遇到的其他格相关问题

HNP问题

可以通过[这篇文章][https://kel.bz/post/hnp/#:~:text=The%20Hidden%20Number%20Problem%20(HNP,compute%20as%20the%20entire%20secret%3F&text=They%20also%20demonstrate%20an%20efficient,a%20significant%20enough%20bit%20leakage.]认识HNP问题，下为简单的测试代码（p需要大于x，但不能超出太多，因为可能会使其本身小于误差值的绝对值）：

from Crypto.Util.number import *
import random


def msb_oracle(x, k, p):
    delta = p >> (k + 1)
    ui = random.randint(x - delta, x + delta)
    return ui


def solve_hnp(t, u, col, k, p): 
    M = Matrix(RationalField(), col, col)
    for i in range(col-1):
        M[i, i] = p
        M[col-1, i] = t[i]

    M[col-1, col-1] = 1 / (2 ** (k + 1))

    def babai(A, w):
        A = A.LLL(delta=0.75)
        G = A.gram_schmidt()[0]
        t = w
        for i in reversed(range(A.nrows())):
            c = ((t * G[i]) / (G[i] * G[i])).round()
            t -= A[i] * c
        return w - t

    closest = babai(M, vector(u+[0]))
    return (closest[-1] * (2 ** (k + 1))) % p


base_1 = 256
base_2 = 270
hidden_num = random_prime(2^base_1, 2^(base_1-1))
p = random_prime(2^base_2, 2^(base_2-1))

n = 30

k = ceil(sqrt(base_2)) + ceil(log(base_2, 2))

t = [random.randint(1, p-1) for i in range(n)]
u = []
for i in range(n):
	u.append(msb_oracle(hidden_num * t[i], k, p))


print(k)
print(solve_hnp(t, u, n+1, k, p))
print(hidden_num)

相关题目writeup链接：

1. 2018 BCTF guess_number
2. 2020 XCTF 高校战役 NHP

相关心得

其实基于LLL算法的Crypto破解本质都是相似的，即构造一个合适的矩阵，其中可能包含题中的已知参数，通过一系列初等变换，找到一个范数较小的向量，将未知数转移到这个小范数向量中，从而求解。

以碰到的一个mix_bag为例：

secret = int(secret.encode('hex'),16)
p = getPrime(2040)
pub = []
key = []
tmp_key = getPrime(1024)
dec_key = getPrime(1024)
enc_key = inverse(dec_key,p)
for _ in range(30):
    key.append(tmp_key)
    pub.append(tmp_key * enc_key % p)
    tmp_key = getPrime(512)

tmp_key = sum(key)

for _ in range(flag.bit_length() - 30):
    tmp_key *= 2
    pub.append(tmp_key * enc_key % p)

with open("data.txt","w") as f:
    f.write("pub = "+str(pub).replace("L","")+"\n")

S = 0

while flag > 0:
    S += (secret & 1) * pub.pop()
    flag >>= 1

with open("data.txt","a") as f:
    f.write("S = " + str(S)+"\n")
    f.write("p = " + str(p))

审题后发现，是一个混合背包，由两部分组成，前30为无序背包，后面则为超递增序列构成的正常背包，但只给了总的和，故需要计算出前面的随机序列key，才能获得flag，根据题意，有：

\[key_i * enc = K_i + T_i * p\]

\(K_i\)（此处K数列即为pub数列前30项）已知，p已知，想到可以构建矩阵，利用格基约化解决问题，构造矩阵如下：

\(p \quad 0 \quad \dots \quad 0 \quad 0 \\ 0 \quad p \quad \dots \quad 0 \quad 0 \\ \vdots \quad \ \vdots \quad \ddots \quad p \quad 0 \\ k_1 \ k_2 \ \ \ \dots \ \ \ k_n \ \ \ x\)

容易发现，在此矩阵构造的格上有二向量（在这种构造的时候，不应该在有限域下去考虑问题）：

\((T_1 p + K_1, \ T_2p+K_2, \ \dots, \ T_np+K_n, \ x)\)

\((key_1 *enc, \ key_2 * enc, \ \dots, \ key_n * enc, \ enc * x)\)

将两向量相减，并把\(key_i * enc = K_i + T_i * p\)代入，则可以得到：

\((0, \ 0, \ \dots, \ 0, (enc - 1) * x)\)

再将此式乘以dec(enc在模p上的逆)，则得到：

\((0, \ 0, \ \dots, \ 0, -dec * x)\)

如果将x的值控制得当，则此向量范数将很小，可以通过LLL得到， 此部分exp如下：

def find_seed(t, col, k, p): 
    # 在有理数域上也可构造格，并使用格基约化
	M = Matrix(RationalField(), col, col)
	for i in range(col-1):
		M[i, i] = p
		M[col-1, i] = t[i]

	M[col-1, col-1] = 1 / (2 ** k)

	final_vector = M.LLL(delta=0.75)[0]
	print(final_vector)
	return (-1 * final_vector[-1] * (2 ** k)) % p
dec = find_seed(pub[:30], 31, 1,p)

其中k的选取不宜过大，较小的值均可找到正确的dec，有了dec之后就变成了简单的背包问题，不再详述。

ECC

Introduction-to-Mathematical Chapter 5

椭圆曲线基础概念

理解椭圆曲线上的基本运算，重点理解O点（所有与y轴垂直线的交点）是为了使椭圆曲线上的加法群完备而虚构的点，为其上加法单位元，至于具体运算公式，如两点相加的泛式等，从原理上理解即可。

至于约束条件，其实本质上是为了使三次方程无解，使得不存在孤立点。

加法规则：

有限域上的椭圆曲线基础概念

Hasse Theorem:

SEA算法可以在较短时间内计算一个椭圆曲线的阶（椭圆曲线上点的个数），在sage中的cypari2模块有集成，ellcard函数和ellsea函数均有涉及，可通过官方文档决定具体使用情况（需要根据有限域的阶是否为素数判断）。

有限域上椭圆曲线的DLP问题

某个点作为生成元的集合的阶是曲线上点集合阶的因子，通过拉格朗日定理易得：

具体证明看75页即可。

The Double-and-Add Algorithm：思想其实就是快速幂算法，在椭圆曲线上，或可称为快速加算法。如果允许三元扩张（即2的幂次的系数不仅可以为0/1，还可以为-1），在期望上会更快，会有\(\frac{3}{2}k +1\) 的上界。

解决ECDLP问题的复杂度为\(O(n^{\frac{1}{2}})\)

Lenstra 算法：利用椭圆曲线的倍数分布分解n，算法的复杂度取决于n最小的因子。

\(2^k\)上的椭圆曲线

注意这里的\(2^k\)不是指椭圆曲线上点的模数为\(2^k\)，而是指其在\(F(2^k)\)上，即k维度的，系数在\(F(2)\)上的向量（即可映射为多项式）。

为了满足之前的无孤立点条件，需要进一步平衡曲线（原因是\(\Delta= -16 (4A^3 + 27B^2)\)，而现在在\(F(2)\)上讨论时前面的系数16即等价于0，则\(\Delta \equiv 0\)）：

平衡后计算规则大体不变，对于一个点的对称点的公式会变为：

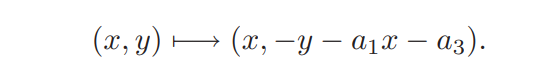
加法公式：

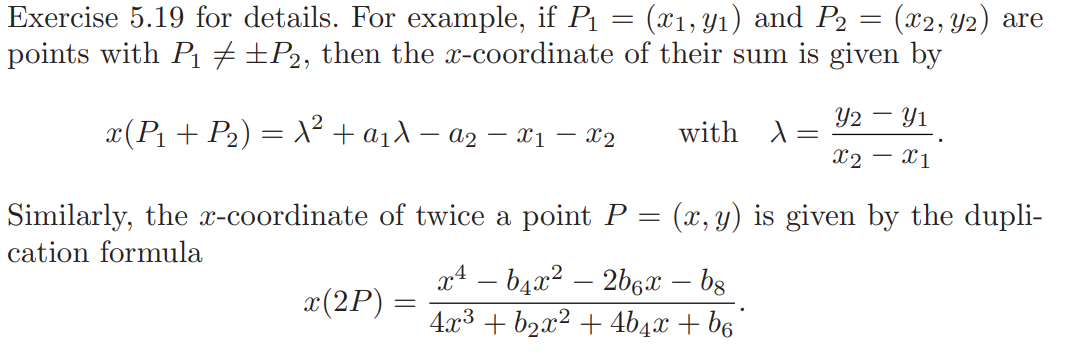
在Koblitz曲线（\(E_a : Y_2 + XY = X^3 + aX^2 + 1\)）上，通过Frobenius映射得到（\(t \leq \sqrt{p}\)应为\(t \leq 2\sqrt{p}\)，且这里\(\alpha,\beta\)的绝对值有误，并不一定为\(\sqrt{p}\)，）：

Frobenius映射提供了一种更高效的计算\(nQ, Q \in E\)的算法，由5.29.(b)可以得到\(\tau^2 = t\tau - p\)

由此可以将n表示为\(n = v_0 + v_1\tau+v_2\tau^2 + \dots + v_l\tau^l\)，使用类似Double-and-Add Algorithm的方法可以在较短时间内计算出\(nQ\)。

Bilinear pairings

双线性对看作一个函数\(f\)的话，其实本质即是对输入\(v, w\) 两个向量，有输出$f(v, w) $ 为一数，且映射\(f\) 对于\(v\) 和\(w\) 都是线性映射。

一个比较泛的例子：

\(A_{n * n}\) 为一n阶方阵，v和w为n阶向量，则\(f(v, w) = v * A * w^t\) 为一\(R^n\) 上的Bilinear pairings

椭圆曲线上，可定义双线性对，先用点阶做一个划分，即有\(E[m] = \{P|mP=O, P \in E\}\)，\(\forall P \in E[m], P = aP_1 + bP_2\)

\(P_1, P_2\) 即 \(E[m]\)上一组基

则对一双线性对\(f\)，有\(f(P_1+P_2, P') = f(P_1, P') \times f(P_2, P')\)

(此处的\(\times\)是未定义算子)

Divisor

对于一个有理多项式\(f(x) = \frac{a\prod_{i=1}^r(X-\alpha_i)^{e_i}}{b\prod_{i=1}^s(X-\beta_i)^{d_i}}\)

其中\(\alpha_i\) 为零点（zeros），\(\beta_i\) 为极点（poles），顾名思义即是让\(f(x) = 0/ \infin\) 的点

定义\(div(f(x)) = \sum_{i=1}^re_i[\alpha_i] - \sum_{i=1}^rd_i[\beta_i]\)

这里的$[_i] \(，并不是一个具体的操作，中括号只是提供一个形式和，即将\)_i, _i\(映射到一个abelian上，从而使得\)div$ 为一个free abelian，具体的映射是不定的，关键在于定义了一个有理多项式上的零点和极点关系的刻画。

对于椭圆曲线E上的\(f\)，有\(div(f) = \sum_{P\in E}n_P [P]\)

其中\(n_P\) 为使得\(P\)为\(f\) zeros/poles的次数，以\(GF(7)\)上曲线 \(E: Y^2= X^3 +1 = (x-6)(x-3)(x-5)\) 为例，其点集为：

image-20201030005553374

可知当x坐标使得\(y=0\) 共有三点，皆不同，故$div(y) = [P_1] + [P_2] + [P_3] - 3O, P_1 =(3,0),P_2 = (5,0),P_3=(6,0) $

这里的分析是考虑对于\(div(f_P) = m[P]-m[O]\) 的情况只有P为\((\alpha, 0)\)此种形式时，\(f_p = X-\alpha\) 才可以满足，因为对于正常的\(P = (\alpha, \beta)\)， 有\(-P = (\alpha, -\beta)\)，故\(div[X-\alpha] = [P] + [-P] - 2[O]\)。

需要注意区分多项式的原始情形和椭圆曲线上的情形，因为多项式原始情形是基于单变量定义的，而椭圆曲线上有两个变量，且使用点来表示div，故存在一些不同，这也是要使用[ ]来做形式和的原因。

Weil pairing

Weil pairing 其实即是定义了一个ECC上的Bilinear pairing，如下

\(e_m(P, Q)\) 的值与\(f_P, f_Q, S\) 无关，他们本质上只是凑出一个自洽的映射

回顾双线性对的定义：

考虑到有\(e_m(aP, bQ) = ab \ e_m(PQ)\)，即等价于第一条。

Weil pairing有性质如下：

1. \(e_m(P,Q)^m = 1 | P, Q\in E[m]\)
2. \(e_m\) 为一双线性对
3. \(e_m(P, P) = 1|P \in E[m]\)， 即\(e_m(P, Q) e_m(Q,P) =1 | P, Q\in E[m]\)
4. 如果对于\(\forall Q \in E[m], e_m(P, Q) = 1\)， 则\(P= O\)

由性质四知，\(\forall P, Q \in E[m], P \not= O, Q\not=O\)，则有\(e_m(P, Q) \not=1\)，即对于双线性对的条件2。

这里可以以前面order为2时的多项式\(f = X-\alpha\)举例：\(\frac{(Q+S).x - \alpha}{S.x-\alpha}/\frac{(P+S).x -\beta}{(-S).x-\beta}\)

仍然以\(GF(7)\)上曲线 \(E: Y^2= X^3 +1 = (x-6)(x-3)(x-5)\) 为例，其点集为：

image-20201030005553374

这里取\(\alpha = 5, P=(5, 0), \beta = 6, Q = (6,0), S = (2, 4)\)

则\((Q+S).x = 0, (P+S).x = 1, S.x =-S.x = 2\)

则\(e_m(P, Q) = \frac{-5}{-3} / \frac{-5}{-4} = \frac{4}{3}\)

取\(S = (4, 3)\)， 则\((Q+S).x = 1, (P+S).x = 0, S.x = -S.x = 4\)

则\(e_m(P, Q) = \frac{-4}{-1}/\frac{-6}{-2} = \frac{4}{3}\)

可知，确实相等，具体的公式推导也可以结合Example5.40理解。

到这里其实可以泛的理解一下，我们定义divsor来刻画极点和零点关系，就是为了构造出\(m[P]-m[O]\)这样的多项式，使其是阶是‘0’，则再构造出来的Weil pairing即是双线性对了

Jacobian Coordinates

Jacobian坐标是不同于仿射坐标的另一种表示椭圆曲线的方式，好处是使得加，乘，求逆等运算的复杂度大幅降低，不过其只能在模为素数的曲线上表示。

Jacobian坐标使用三个分量\((X, Y, Z)\)，对应仿射坐标中的\((\frac{X}{Z^2}, \frac{Y}{Z^3})\)，之前其实一直也有些疑惑为什么sage中的椭圆曲线坐标都是\((x,y,1)\)，现在才知道其实这是取Z=1，则前两个分量等同于在仿射坐标系下的值。Jacobian坐标下的add和double提供了更低复杂度的算法，通常我们先将仿射坐标系的点转化为Jacobian坐标下的点，计算结束后再转为仿射坐标。

具体算法参见wiki 。

超椭圆曲线

椭圆曲线为亏格等于1的代数曲线，而超椭圆曲线指亏格大于1的代数曲线，但仅有亏格为2的超椭圆曲线有与椭圆曲线相同的安全性。

推荐看这篇文章，对超椭圆曲线的基础概念介绍的非常详细（可以只看1，2，5，9章，即可有个大概了解了）。

超椭圆曲线定义如下，其天然不存在孤立点：

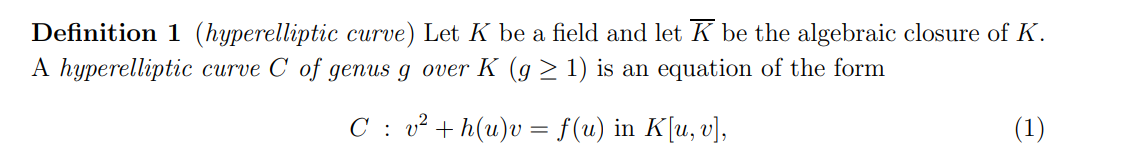
Jacobian variety

超椭圆曲线上的加法群完备性源自于其Jacobian variety（雅克比簇）加法群为Abelian group，其点的运算也是需要先转化为Jacobian variety后再运算，环Jacobian variety的阶记为\(\#J\)，即类似于\(GF(n)\)上欧拉函数的意义。

\(\#J\) 是基于超椭圆曲线的密码学中重要的安全参数，有如下限制：

其计算方法如下（此为亏格为2的情况，其余情况类比即可，其中\(M_i\) 为\(F_{q^i}\)下曲线阶数）：

化为代码（使用的曲线为TCTF2020 Simple Curve）如下：

# Paramters and curve
q = 2
n = 256
genus = 2
# h(x) = x^2 + x
# f(x) = x^5 + x^3 + 1
h = lambda x: x ^ 2 + x
f = lambda x: x ^ 5 + x ^ 3 + 1

# Calc M_i
M = []

for i in range(genus):
    P.<x> = PolynomialRing(GF(q ^ (i + 1)))
    C = HyperellipticCurve(f(x), h(x))
    M.append(C.cardinality())
print("Calc M done")

# Calc a_i
a = [0]
for i in range(genus):
    a.append((M[i] - 1 - q ^ (i + 1) + a[i] ^ (i + 1)) / (i + 1))
a = [1] + a[1:]
print("Calc a done")

# Calc gamma_i
var('X')
function = -genus * q
for i in range(genus + 1):
    function += a[i] * X ^ (genus - i)
gamma = list(map(lambda x: x.rhs(), solve([function == 0], X)))
print("Calc gamma done")

# Calc alpha_i
alpha = []
for i in range(genus):
    function = X ^ 2 - gamma[i] * X + q
    alpha.append(list(map(lambda x: x.rhs(), solve([function == 0], X))))
print("Calc alpha done")

# Calc #J
order = 1
for i in range(genus):
    order *= abs(1 - alpha[i][0] ^ n) ^ 2
print('#J =', int(order))

Stream

PRNG

LCG

已知（a，b，m）的直接通过解同模方程就行（方法很多，也可以利用格），已知（a，b），但m未知可以通过淘宝师傅博客的方法：

也比较简单，至于有截断的泄露，其实就是普通的HNP问题，直接套用HNP脚本求解即可，附上NPUCTF2020中baby_LCG的求解seed部分exp：

key = {'b': 153582801876235638173762045261195852087, 'a': 107763262682494809191803026213015101802, 'm': 226649634126248141841388712969771891297}
data = [7800489346663478448,
            11267068470666042741,
            5820429484185778982,
            6151953690371151688,
            548598048162918265,
            1586400863715808041,
            7464677042285115264,
            4702115170280353188,
            5123967912274624410,
            8517471683845309964,
            2106353633794059980,
            11042210261466318284,
            4280340333946566776,
            6859855443227901284,
            3149000387344084971,
            7055653494757088867,
            5378774397517873605,
            8265548624197463024,
            2898083382910841577,
            4927088585601943730]

u = []
for i in range(19):
	u.append((data[i+1] - data[i]) << 64)

t = []
for i in range(19):
	t.append(key['a'] ** i)

k = 64
n = 19
print(solve_hnp(t, u, n+1, k, key['m']))

其中的solve_hnp函数即是我之前HNP示例中的函数。

梅森旋转

如果是已知624位以上的序列，可以直接使用rand_crack破解，如果知道的序列下标之间有\(a \equiv (b + t) \mod(m)\)（其中m为梅森旋转的状态数，t为旋转步骤中的参数），则也可以破解，具体例题可参见NPUCTF2020 Mersenne twister，exp如下：

from hashlib import *
from itertools import *
from binascii import hexlify , unhexlify
from z3 import *
from Crypto.Util.number import *


XOR = lambda s1 ,s2 : bytes([x1 ^ x2 for x1 ,x2 in zip(s1 , s2)])


class mt73991:
    def __init__(self , seed):
        self.state = [seed] + [0] * 232
        self.flag = 0
        self.srand()
        self.generate()

    def srand(self):
        for i in range(232):
            self.state[i+1] = 1812433253 * (self.state[i] ^ (self.state[i] >> 27)) - i
            self.state[i+1] &= 0xffffffff

    def generate(self):
        for i in range(233):
            y = (self.state[i] & 0x80000000) | (self.state[(i+1)%233] & 0x7fffffff)
            temp = y >> 1
            temp ^= self.state[(i + 130) % 233]
            if y & 1:
                temp ^= 0x9908f23f
            self.state[i] = temp

    def getramdanbits(self):
        if self.flag == 233:
            self.generate()
            self.flag = 0
        bits = self.Next(self.state[self.flag]).to_bytes(4, 'big')
        self.flag += 1
        return bits

    def get_random_num(self):
        if self.flag == 233:
            self.generate()
            self.flag = 0
        num = self.state[self.flag]
        self.flag += 1
        return num

    def Next(self , tmp):
        tmp ^= (tmp >> 11)
        tmp ^= (tmp << 7) & 0x9ddf4680
        tmp ^= (tmp << 15) & 0xefc65400
        tmp ^= (tmp >> 18) & 0x34adf670
        return tmp


def encrypt(key , plain):
    tmp = md5(plain).digest()
    return hexlify(XOR(tmp , key))


def decrypt(c, m):
    tmp = md5(m).digest()
    bits = XOR(tmp, c)
    return [bytes_to_long(bits[4 * _:4 * (_+1)]) for _ in range(4)]


def true_decrypt(c, key):
    tmp = XOR(c, key)
    for a in range(0x20, 0x7f):
        if md5(chr(a).encode()).digest() == tmp:
            return chr(a)
    return '\x00'


__kMaxBits = 0xffffffff


def __inverse_right_shift_xor(value, shift, mask):

    i, result = 0, 0
    while i * shift < 32:
        part_mask = ((__kMaxBits << (32 - shift)) & __kMaxBits) >> (i * shift)
        part = value & part_mask
        if mask != 0:
            value ^= (part >> shift) & mask
        else:
            value ^= part >> shift
        result |= part
        i += 1
    return result


def __inverse_left_shift_xor(value, shift, mask):
    i, result = 0, 0
    while i * shift < 32:
        part_mask = (__kMaxBits >> (32 - shift)) << (i * shift)
        part = value & part_mask
        value ^= (part << shift) & mask
        result |= part
        i += 1
    return result


def from_mt_to_state(tmp):
    tmp = __inverse_right_shift_xor(tmp, 18, 0x34adf670)
    tmp = __inverse_left_shift_xor(tmp, 15, 0xefc65400)
    tmp = __inverse_left_shift_xor(tmp, 7, 0x9ddf4680)
    tmp = __inverse_right_shift_xor(tmp, 11, 0xffffffff)
    return tmp


def guess(state_103, state_0):
    possible = state_103
    possible ^= state_0
    if possible.bit_length() > 31:
        possible ^= 0x9908f23f
    possible <<= 1
    return possible


def final_inverse(enc):
    tmp = enc & 0x7fffffff
    return tmp | (0x7fffffff+1), tmp


def inverse_srand(value, i):
    value += i
    value *= inverse(1812433253, 0xffffffff+1)
    value = __inverse_right_shift_xor(value, 27, 0xffffffff)
    return value


def find_init_seed(state_103):
    last_state = state_103
    for i in range(103, -1, -1):
        last_state = inverse_srand(last_state, i)
    return last_state


if __name__ == "__main__":

    flag_start = 'npuctf{'
    flag_end = '}'
    cipher = unhexlify(open("cipher.txt", "rb").read())
    random = []
    for i in range(7):
        random.extend(decrypt(cipher[16 * i: 16 * (i+1)], flag_start[i].encode()))
    print(random)

    state = []
    for i in range(28):
        state.append(from_mt_to_state(random[i]))
    print(state)

    random_last = decrypt(cipher[-1*16:], flag_end.encode())
    state_last = [from_mt_to_state(i) for i in random_last]

    # print(state_last)
    mid = guess(state_last[-1], state[0])
    old_104 = []
    old_104.extend(final_inverse(mid))
    if inverse_srand(old_104[0], 103) & 0x80000000 == mid & 0x80000000:
        if inv_srand(old_104[1], 103) & 0x80000000 == mid & 0x80000000:
            print("two cases found")
        else:
            old_104 = old_104[0]
    else:
        old_104 = old_104[1]

    print('old state 104 = ' + str(old_104))

    seed = find_init_seed(old_104)
    print('seed = ' + str(seed))

    random = mt73991(seed)
    flag = ''
    for i in range(26):
        tmp = b''
        for j in range(4):
            tmp += random.getramdanbits()
        flag += true_decrypt(cipher[16 * i: 16 * (i+1)], tmp)
    print(flag)

LFSR

Given n bits, mask

如果可以泄露LFSR的n位并且知晓抽头序列，则可以直接破解，方法可以参见这篇博客，给出通用的exp：

def inverse_lfsr(out, mask):
    out = out[::-1]
    mask = mask[::-1]
    index = []
    for i in range(len(mask)):
        if mask[i] == '1':
            index.append(i)
    print(index)
    for i in range(len(out)):
        mid = int(out[0])
        for j in range(len(index)-1):
            mid ^= int(out[index[j]+1])
        out = out[1:] + str(mid)
    return out[::-1]

NLFSR

n个LFSR并行，最终结果通过每个LFSR输出的代数运算获得密钥流，设输入为\(a_1, \dots, a_n\)，输出为\(b\)，则\(p_i = P\{a_i=b\}\)，则当\(p_i\)较大时（大于0.6即可），我们可以通过足够多的密钥流，通过统计找到概率相近的，作为备选值，之后依次爆破即可，可参见De1CTF2020 NLFSR的exp。

Given 2n bits

如果已知至少2n位的密钥流，但不知道抽头序列，则即为KPA问题，因为只要把前n个bit \(a_1,\dots,a_n\)看成原本状态，则对后n个bit \(b_1, \dots, b_n\)均有\(b_i = \sum_{i=1}^{n}a_i\&p_i\)，\(p_i\)即为抽头序列，有n个这样的表达式，即为解n元一次方程，故而一定有解，通用exp如下（其中inverse_lfsr即为之前例子中函数）：

def init_stream(known_plain, known_cipher):
    assert(len(known_plain) == len(known_cipher) and len(known_plain) <= 24)
    known_plain_dec = int(known_plain, 16)
    known_cipher_dec = int(known_cipher, 16)
    return bin(known_plain_dec ^ known_cipher_dec)[2:].rjust(4 * len(known_plain), '0')


def lfsr_crack_key(stream, key_length, p):
    assert(len(stream) >= 2 * key_length)
    solver = Solver()
    for i in range(len(stream) - key_length):
        cur = stream[i: i + key_length + 1]
        equation = ''
        for j in range(key_length):
            if cur[j] == '1':
                equation += 'p[' + str(j) + ']+'
            else:
                pass
        if len(equation):
            equation = equation[:-1] + ' == ' + str(cur[-1])
            solver.add(eval(equation))
    if solver.check() == sat:
        m = solver.model()
        feedback = ''.join([str(m[p[i]]) for i in range(key_length)])
        return stream[:key_length], feedback
    else:
        return False, False


def inverse_lfsr_kpa(stream):
    for key_length in tqdm(range(2, len(stream)//2 + 1)):
        p = []
        for i in range(32):
            p.append('p%d' % i)
        p = [BitVec(i, 1) for i in p]
        key, mask = lfsr_crack_key(stream, key_length, p)
        if (key, mask) != (False, False):
            return inverse_lfsr(key, mask)

Block

推荐书目：《分组密码攻击实例》

咕咕咕

推荐题单

题目	考点	难度(?/100)
De1CTF2020 ECDH	筛法构造低阶椭圆曲线--ECC	60
De1CTF2020 NLFSR	根据布尔表达式计算概率--Stream	35
RCTF2020 infant_ECC	多元Copper Smith--ECC	70
SCTF2020 Lattice	基础NTRU攻击--Lattice	30
NCTF2019 easy_RSA	有限域开高次方--AMM algorithm	60
watevrCTF2019 Swedish_RSA	多项式上的RSA--RSA&Polynomial	30
watevrCTF2019 ECC_RSA	多项式分解--ECC&RSA	50
MIXCTF2020 mix_bag	HNP--Knapsack	65
NPUCTF2020 baby_LCG	HNP--PRNG（可以先做这道，再做上面的）	55
NPUCTF2020 Mersenne twister	梅森旋转--PRNG	55
WMCTF2020 piece_of_a_cake	NTRU攻击&私钥重复攻击--Lattice	65
天翼杯2020 hard_RSA	Copper Smith--RSA	40