Lord Riot's Blog
0%

杂题闲记

发表于 更新于 分类于
强网杯\安恒八月赛

此系列博客主要记录一下一些题的做题想法（各种rz心路历程orz

强网杯

proof for dice2cry

本质上即是partial oracle mod 3

根本问题在于对于\((3 *m \mod n) \mod 3\)，是否可以根据模数判断m所在区间，即属于\((0, \frac{1}{3}n), (\frac{1}{3}n, \frac{2}{3}n), ( \frac{2}{3}n,n)\) 中的哪一个。

case 0：

如果模3的结果为0，那么其实可以很容易的知道\(3*m\)并没有被截断，故而属于$ (0, n)$ 区间

case 1/2：

对于模数为1或2的情况，并不存在一定的一一对应的解区间，但对于相同的n，1/2对应的区间是一定的，下面给出第二区间的证明（第三区间类似）：

$m (n, n), (3 *m -n) x ,  x = 1  or  2 $

使用反证法，不妨设

\(\exists \ m_1, m_2 ,\\\ (3 * m_1 -n) \equiv x_1 \mod 3 , \quad (3 *m_2 -n) \equiv x_2 \mod 3 ,\\\ x_1 \neq x_2\)

两式相减得到

\(\Rightarrow 3 * (m_1 - m_2) \equiv x_3 \mod 3, x_3 \neq 0\)

又因为

\(3 | 3 *(m_1-m_2)\)

故\(3 * (m_1-m_2) \equiv 0 \mod 3\)，假设错误，命题得证。

安恒8月赛

这次的crypto貌似是shallow，tb还有coin出的。。。确实有水平，比赛的时候只有LCG那个比较有思路，另外俩个有点懵。。感觉这几个题出到月赛有点浪费hh，时间太短，做出来的人并不多

math stream

观察得到LCG的迭代关系为\(k_i \equiv a * k_{i-2} + (a + 1) * k_{i-1} + c \mod n\)

然而相关参数\(n, c, a\) 一个都没给，只给出了301到307这6个生成数据，需要我们预测最后一个数据，发现数列长度\(2^{1024}\)，于是考虑可以使用矩阵快速幂（复杂度\(O(logn)\)）。

计算通项公式：

待定系数x，y，z，则有\(k_i - x * k_{i-1} + z * c \equiv y*(k_{i-1} - x * k_{i-2} + z * c) \mod n\)

可知：

\(x + y = a+1 ,\\\ -x * y = a ,\\\ (y-1)* z = 1\)

得到：

\(x = \frac {a + 1 + \sqrt {a^2 + 6a + 1} }{2} ,\\\ y = \frac {a + 1 - \sqrt {a^2 + 6a + 1} }{2} ,\\\ z = \frac {2 }{a - 1 - \sqrt {a^2 + 6a + 1} }\)

设\(s_i = k_i - x * k_{i-1} + z * c \mod n\)，则可知\(s_i\)为\(GF(n)\)上的等比数列，

有 \(s_{i+2} = y ^ i(k_2 -x * k_1 + z *c) \mod n\)，\(k_1, k_2\)即为初始生成的随机种子

有\(k_{i+2} = x^i*k_2 + (k_2 -x * k_1 + z *c)*\sum_{j=0}^{i}x^jy^{i-j} - z*c*\sum_{j = 0}^{i-1}x^j\)

上面是我做题时的错误路线，我一开始以为是纯数列题orz

构造格子

通过上面的通项公式可以发现，想要将数列的二阶公式降到一阶需要让参数变的异常复杂，故直接使用二阶公式作为来构造格子

\(k_i \equiv a * k_{i-2} + (a + 1) * k_{i-1} + c \mod n\)

\(\Rightarrow k_i - k_{i-1} \equiv a * (k_{i-2} + k_{i-1}) + c \mod n\)

\(\Rightarrow k_i - k_{i-1} = a * (k_{i-2} + k_{i-1}) + c +T *n, \quad T \in Z\)

由于对\(a,c, n\) 一无所知，故只能使用四组\(k_i - k_{i+1}, k_{i-2} + k_{i-1}\) 构造格子

设\(fini_{i} = k_{i+2}-k_{i}, init_i = k_i + k_{i+1}\)

则有$fini_i = a * init_i + c + T_i * n $

于是我构造了如下格子：

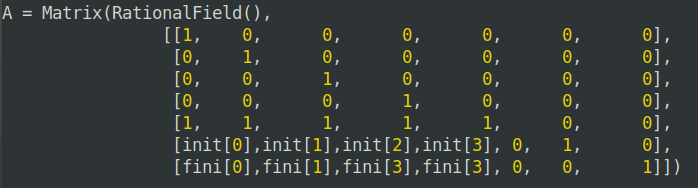
但前四行的最后一列并无法平衡，因为需要找到\(B_0, B_1, B_2, B_3\) 使得\(\sum_{i=0}^{4}B_i*(fini_i-a*init_i-c) << min{B_i}\)， 而我们并不知道\(a,c\)，构造出这样的\(B_i\)，显然是不可能的，但如果我们能求出n，那么只需将对角线上的1替换为n，即可解决问题。

然后在求解n的过程中，我意识到完全不用格子ojz，直接推就能推出来。。。而且将n代入也未能求解。。。

推导求解

由之前推导的\(k_i - k_{i-1} \equiv a * (k_{i-2} + k_{i-1}) + c \mod n\)

则有 \((k_i - k_{i-1}) - (k_{i-1} - k_{i-2}) \equiv a *(k_{i-1} - k_{i-3}) \mod n\)

由此，只要知道了n，则可以计算出a，c

根据同模，利用最大公因数来求n

利用$(k_{i-2} - k_{i-4}) * (a *(k_{i-1} - k_{i-3}) n) $

$ (k_{i-1} - k_{i-3}) * (a *(k_{i-2} - k_{i-4}) n) n$

此部分exp如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def get_f(k, i):
    assert len(k) > i-4 >= 0
    return abs((k[i] - 2 * k[i-1] + k[i-2]) * (k[i-2] - k[i-4]) - (k[i-1] - k[i-3]) * (k[i-1] - 2 * k[i-2] + k[i-3]))


f_1 = get_f(k, 4)
f_2 = get_f(k, 5)

n = gcd(f_1, f_2)
print('n = ' + str(n))
assert isPrime(n)

a = ((k[3] - 2 * k[2] + k[1]) * inverse(k[2] - k[0], n)) % n
print('a = ' + str(a))

c = ((k[2] - k[1]) - a * (k[0] + k[1])) % n
print('c = ' + str(c))

这里我起初是想使用最早的通项公式，但是发现，那个方程在模n下无解。。于是只能使用矩阵快速幂来做计算

完整exp如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
from Crypto_tools import *

target = 2 ** 1024
k = 

cipher = 


def get_f(k, i):
    assert len(k) > i-4 >= 0
    return abs((k[i] - 2 * k[i-1] + k[i-2]) * (k[i-2] - k[i-4]) - (k[i-1] - k[i-3]) * (k[i-1] - 2 * k[i-2] + k[i-3]))


f_1 = get_f(k, 4)
f_2 = get_f(k, 5)

n = gcd(f_1, f_2)
print('n = ' + str(n))
assert isPrime(n)

a = ((k[3] - 2 * k[2] + k[1]) * inverse(k[2] - k[0], n)) % n
print('a = ' + str(a))

c = ((k[2] - k[1]) - a * (k[0] + k[1])) % n
print('c = ' + str(c))

initial_stream = [[k[5], k[4], 1],
                  [0,    0,    0],
                  [0,    0,    0]]
initial_coefficient = [[a+1, 1, 0],
                       [a,   0, 0],
                       [c,   0, 1]]


final_coefficient = matrix_pow(initial_coefficient, 3, target-305, n)
final_stream = matrix_mul(initial_stream, final_coefficient, 3, n)
key = int(final_stream[0][1]) % n
flag = cipher ^ key
print(long_to_bytes(flag))

Lattice_trick

本题考查的是利用格来辅助解方程的技巧，题给了两个等式：

\(p * q = n\)

\(11^{2020} p^2 + 45^{2020}q^2 \equiv m \mod N\)

根本的困难在于第二个式子中的因子太大，利用sage无法直接求解模方程，我起初是想通过化简式子或是直接将等式搬到格上，但都没有成功，最终看了badmonkey师傅的exp才意识到可以只利用格子来降低参数，将有限域转化为整数域，再使用sage等工具解方程。

抽象问题为寻找到整数A，使得\(a * 11^{2020} p^2 + a*45^{2020}q^2 \equiv b_1p^2 + b_2q^2 \mod N\)

且\(b_1, b_2\) 较小，此处不难想到可以构造格子，使\(b_1, b_2\) 为格子上SVP即可。

我尝试过构造：

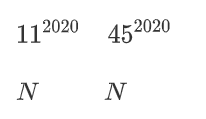
但由于\(11^{2020}\)本身的位数过大，LLL后的GapSVP会直接返回\((N, N)\)向量，故需要做一些转换（此处的\(11^{-2020}\)为\(11^{2020}\)在N上的模逆）：

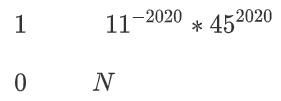
由此即可得到向量\((a_1, a_2)\)，有\(a * 11^{2020} p^2 + a*45^{2020}q^2 \equiv a_1p^2 + a_2q^2 \mod N\)

且 \(a = a_1 * 11^{-2020},\quad a_2 \equiv a1 * 11^{-2020}*45^{2020} \mod N\)

分析一下p，q的位数，都是512位，故而\(p^2 \ or \ q^2\) 的位数也不会超过1024，而求得的\(a_1, a_2\)中最大的为1023位，可知\(a_1p^2 + a_2q^2\) 最大位数为\(1024 + 1 + 1023 = 2048\)，而N的位数为2048，故而只需让k遍历-1到1，必然存在\(a_1p^2 + a_2q^2 = k *m + (a_1p^2 + a_2q^2) \% N\)

又有：

\((a_1p^2 + a_2q^2) \% N = ((a_1 * 11^{-2020}) * (11^{2020} p^2 + 45^{2020}q^2) \% N) \% N\)

即可与\(p * q = n\) 联立求解，完整exp如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
from Crypto.Util.number import *
from sage.all import *

r = 
n,h,N = 
c = 
e = 65537
h = (h-pow(14, 2020, N) * (r**2))%N


def Reduce(n,m,h):
    inv = (45**2020)*inverse(11**2020,m)
    lattice = Matrix([
        [1,inv],
        [0,m]
    ])

    res = lattice.LLL()
    a1 = int(res[0,0])
    a2 = int(res[0,1])
    
    if a1<0:
        a1,a2 = -a1,-a2%m
    print('a1 = ' + str(a1))
    print('a2 = ' + str(a2))
    
    tmp = int(a1*inverse(11**2020,m)*h)%m
    x = var('x')
    y = var('y')

    for i in range(-1,2):
        cur = tmp + i*m
        eq1 = x*y==n
        eq2 = a2*x**2 + a1*y**2 - cur == 0
        res = solve([eq1,eq2],x,y, solution_dict=True)
        if len(res) > 2:
            print("Got the solution")
            print(res[-1])
            return int(abs(res[-1][x])), int(abs(res[-1][y]))
        print("No solution for %d"%i)

p, q = Reduce(n//r, N ,h)

phi = (p-1)*(q-1)*(r-1)
d = inverse(e, phi)
c = bytes_to_long(c)
m = pow(c,d,n)
print(long_to_bytes(m))
Copper_smith_e_d

已知：

\(n = p * q * r ,\\\ r ,\\\ e * d \equiv 1 \mod ((p-1)*(q-1)*(r-1)) ,\\\ d^e \equiv t \mod n ,\\\ e = 3\)

可以看到e非常的小为3，故可知\(e *d = 1 + k * (p-1)(q-1)(r-1)\) 中k小于3，使k遍历1，2，即可得到等式\(e *d = 1 + k * (p-1)(q-1)(r-1)\)， 再将\(d^3 \equiv t \mod n\) 变为\((e * d )^3 \equiv 27 t \mod n\)

从而得到方程：\((1 + k * (p-1)(q-1)(r-1))^3 \equiv 27t \mod n\)

可化简为\((1 + k*(r-1)*(p*q -(p+1) +1))^3 \mod 27 t \mod n\)

有单变量\(p+q\)，分析\(p+q\) 的位数最大为1025位，而n的位数为3344， 代入Copper_smith参数

即为：\[\beta = 1, \delta = 3, p+q \leq \frac{1}{2}n^{\frac{1}{3} - \epsilon} \]

可近似为\(2 ^ {1025} - 1 \leq \frac{1}{2}n^{\frac{1}{3} - \epsilon}\)

此处也可以随机取两个位数为1024的素数之和近似p+q，将\(\frac{1}{3} - \epsilon\) 看作\(\frac{a}{b}\)，找到满足满足\((2 * (p+q))^b < n ^a\)中\(\frac{a}{b}\)最小的，则\(\epsilon = \frac{1}{3} - \frac{a}{b}\)， 寻找代码如下：

1
2
3
4
5
6
7
8
9
10
for i in range(10):
    p = getPrime(1024)
    q = getPrime(1024)
    base = 2 * (p+q)
    tmp = []
    for i in range(1, 100):
        for j in range(1, 100):
            if base ** i < n ** j:
                tmp.append(j/i)
    print(1/3 - min(tmp))

\(2^{1025}\)的寻找结果为0.025

随机\(p, q\)寻找的结果约为0.026，（最终求解后验证得\(\epsilon\) 约为0.0265）

可知\(\epsilon > 0.026\)，取0.03，将参数代入smallroots求解方程即可得到\(p+q\)， 从而得到phi，得到flag，完整exp如下（取0.03时计算时间过长。。。改成0.035或0.04之后很快就出了。。似乎越大越快（迷惑？））：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from Crypto.Util.number import *


n = 
c = 
r = 
t = 

PR.<x> = PolynomialRing(Zmod(n))
e_d_3 = (27 * t) % n
p_q = n//r

for k in range(1, 3):
	f = (1+k*(r-1) * (p_q-x+1))^3 - e_d_3
	solve_1 = f.monic().small_roots(X=2^1025, beta=1, epsilon=0.04)
	if len(solve_1) > 0:
		p_add_q = solve_1[0]
		phi = (r-1) * (p_q-p_add_q+1)
		d = inverse(3, phi)
		flag = long_to_bytes(pow(c, d, n))
		print(flag)